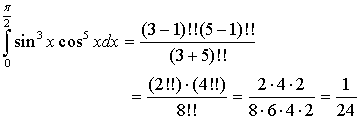§5.5
定积分的分部积分法
设函数![]() ,
,![]() 在区间
在区间![]() 上具有连续的导函数, 则
上具有连续的导函数, 则
![]()
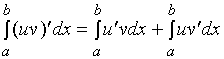
而
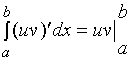
故
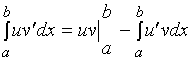
这就是定积分的分部积分公式。
也可写成形式 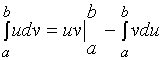
【例1】求 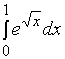
解:
令 ![]() ,
, ![]() ,
, ![]()
当 ![]() 时,
时, ![]() ; 当
; 当 ![]() 时,
时, ![]() 。
。
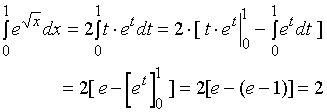
【例2】计算定积分 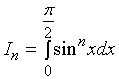 (
( ![]() 为自然数 )。
为自然数 )。
解:设
![]() ,
,
![]()
![]() ,
, ![]()
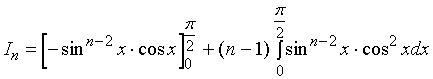
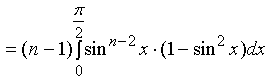
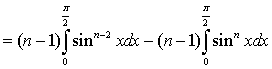
![]()
![]()
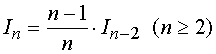
这样,我们得到了递推公式,依此公式,再计算出两个简单的初值![]() 与
与![]() ,即可求得
,即可求得![]() 。
。
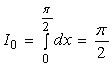 ,
, 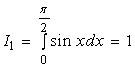
当
![]() 为偶数,有
为偶数,有
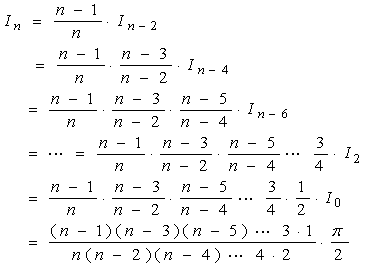
引入记号
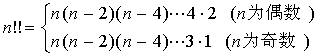
![]()
同理,若![]() 为奇数,有
为奇数,有
![]()
综合便得到著名的华里斯公式一
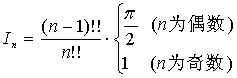
由于
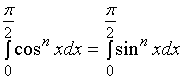 , 故
, 故
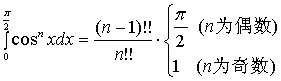
【例3】求 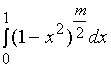 (
( ![]() 为自然数 )
为自然数 )
解:令![]() ,
, ![]()
当![]() 时,
时, ![]() ; 当
; 当 ![]() 时,
时, ![]()
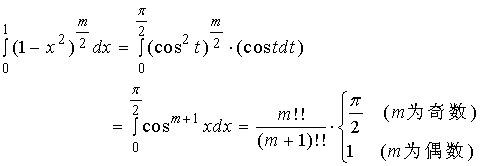
【例4】(华里斯公式二)
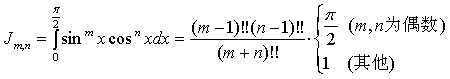
证明:设 ![]()
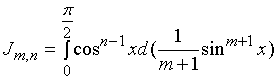
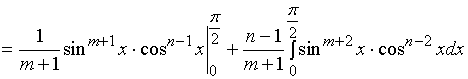
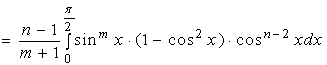
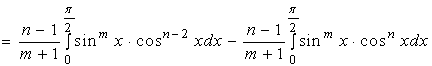
![]()
![]()
![]()
当
![]() 时, 有
时, 有
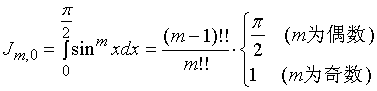

如果
![]() 为偶数, 则有
为偶数, 则有
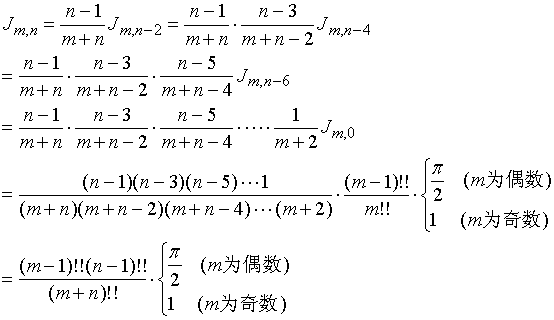
如果
![]() 为奇数,则
为奇数,则
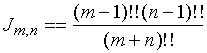
综合得到著名而常用的华里斯公式二
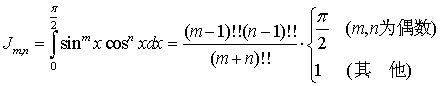
华里斯公式的应用十分地广泛,掌握好它可以方便地求许多定积分。
【例5】求 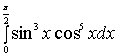
解:应用华里斯公式二, 有